经典面试题:如何寻找最⻓回文子串
经典面试题:如何寻找最⻓回文子串
预计阅读时间:5 分钟
回文串是面试常常遇到的问题(虽然问题本身没啥意义),本文就告诉你回文串问题的核心思想是什么。
首先,明确一下什:回文串就是正着读和反着读都一样的字符串。
比如说字符串aba和abba都是回文串,因为它们对称,反过来还是和本身一样。反之,字符串abac就不是回文串。
可以看到回文串的的长度可能是奇数,也可能是偶数,这就添加了回文串问题的难度,解决该类问题的核心是双指针。下面就通过一道最长回文子串的问题来具体理解一下回文串问题:
1 | string longestPalindrome(string s) {} |
一、思考
对于这个问题,我们首先应该思考的是,给一个字符串s,如何在s中找到一个回文子串?
有一个很有趣的思路:既然回文串是一个正着反着读都一样的字符串,那么如果我们把s反转,称为s',然后在s和s'中寻找最长公共子串,这样应该就能找到最长回文子串。
比如说字符串abacd,反过来是dcaba,它俩的最长公共子串是aba,也就是最长回文子串。
但是这个思路是错误的,比如说字符串aacxycaa,反转之后是aacyxcaa,最长公共子串是aac,但是最长回文子串应该是aa。
虽然这个思路不正确,但是这种把问题转化为其他形式的思考方式是非常值得提倡的。
下面,就来说一下正确的思路,如何使用双指针。
寻找回文串的问题核心思想是:从中间开始向两边扩散来判断回文串。对于最长回文子串,就是这个意思:
1 | for 0 <= i < len(s): |
但是呢,我们刚才也说了,回文串的长度可能是奇数也可能是偶数,如果是abba这种情况,没有一个中心字符,上面的算法就没辙了。所以我们可以修改一下:
1 | for 0 <= i < len(s): |
PS:读者可能发现这里的索引会越界,等会会处理。
二、代码实现
按照上面的思路,先要实现一个函数来寻找最长回文串,这个函数是有点技巧的:
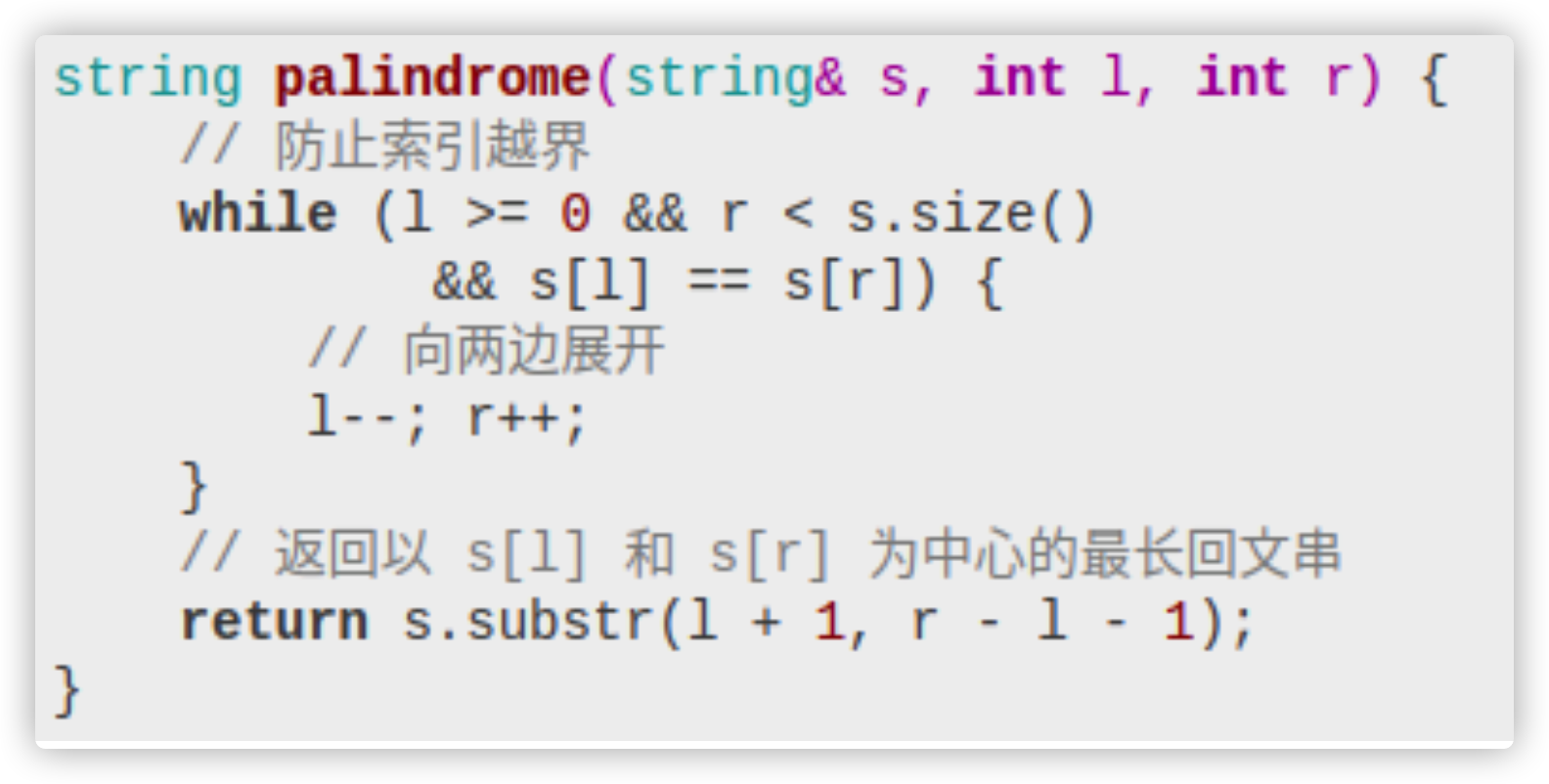
为什么要传入两个指针l和r呢?因为这样实现可以同时处理回文串长度为奇数和偶数的情况:
1 | for 0 <= i < len(s): |
下面看下longestPalindrome的完整代码:
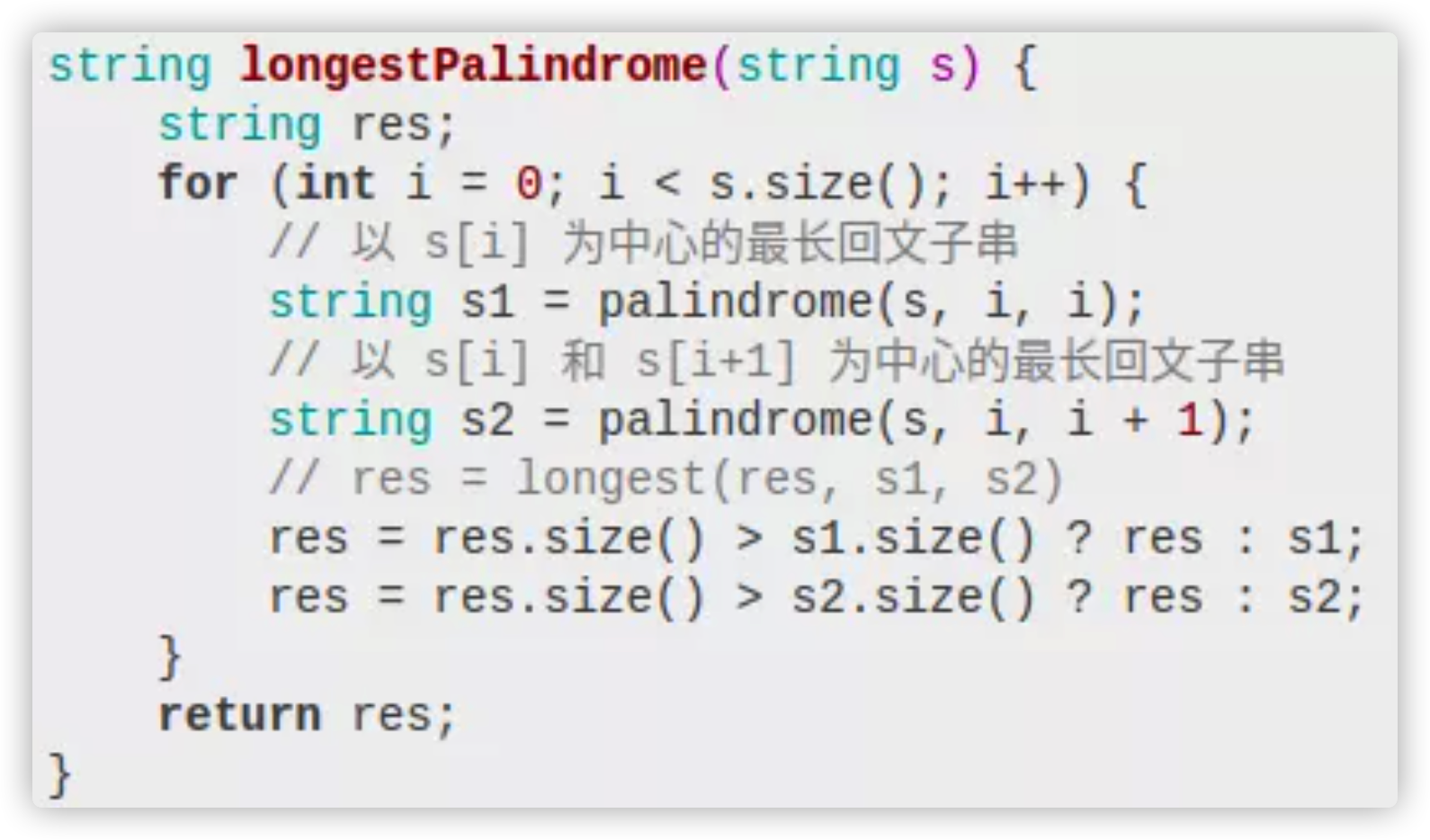
至此,这道最长回文子串的问题就解决了,时间复杂度 O(N^2),空间复杂度 O(1)。
值得一提的是,这个问题可以用动态规划方法解决,时间复杂度一样,但是空间复杂度至少要 O(N^2) 来存储 DP table。这道题是少有的动态规划非最优解法的问题。
另外,这个问题还有一个巧妙的解法,时间复杂度只需要 O(N),不过该解法比较复杂,我个人认为没必要掌握。该算法的名字叫 Manacher’s Algorithm(马拉车算法),有兴趣的读者可以自行搜索一下。