回溯算法团灭排列组合子集问题
回溯算法团灭排列/组合/子集问题
回溯算法团灭排列/组合/子集问题
预计阅读时间:7 分钟
今天就来聊三道考察频率高,而且容易让人搞混的算法问题,分别是求子集(subset),求排列(permutation),求组合(combination)。这几个问题都可以用回溯算法解决。
一、子集
问题很简单,输入一个不包含重复数字的数组,要求算法输出这些数字的所有子集。
1 | vector<vector<int>> subsets(vector<int>& nums); |
比如输入 nums = [1,2,3],你的算法应输出 8 个子集,包含空集和本身,顺序可以不同:
[ [],[1],[2],[3],[1,3],[2,3],[1,2],[1,2,3] ]
第一个解法是利用数学归纳的思想:假设我现在知道了规模更小的子问题的结果,如何推导出当前问题的结果呢?
具体来说就是,现在让你求 [1,2,3] 的子集,如果你知道了 [1,2] 的子集,是否可以推导出 [1,2,3] 的子集呢?先把 [1,2] 的子集写出来瞅瞅:
[ [],[1],[2],[1,2] ]
你会发现这样一个规律:
subset([1,2,3]) - subset([1,2])
= [3],[1,3],[2,3],[1,2,3]
而这个结果,就是把 sebset([1,2]) 的结果中每个集合再添加上 3。
换句话说,如果 A = subset([1,2]) ,那么:
subset([1,2,3])
= A + [A[i].add(3) for i = 1..len(A)]
这就是一个典型的递归结构嘛,[1,2,3] 的子集可以由 [1,2] 追加得出,[1,2] 的子集可以由 [1] 追加得出,base case 显然就是当输入集合为空集时,输出子集也就是一个空集。
翻译成代码就很容易理解了:
1 | vector<vector<int>> subsets(vector<int>& nums) { |
这个问题的时间复杂度计算比较容易坑人。我们之前说的计算递归算法时间复杂度的方法,是找到递归深度,然后乘以每次递归中迭代的次数。对于这个问题,递归深度显然是 N,但我们发现每次递归 for 循环的迭代次数取决于 res 的长度,并不是固定的。
根据刚才的思路,res 的长度应该是每次递归都翻倍,所以说总的迭代次数应该是 2^N。或者不用这么麻烦,你想想一个大小为 N 的集合的子集总共有几个?2^N 个对吧,所以说至少要对 res 添加 2^N 次元素。
那么算法的时间复杂度就是 O(2^N) 吗?还是不对,2^N 个子集是 push_back 添加进 res 的,所以要考虑 push_back 这个操作的效率:
1 | vector<vector<int>> res = ... |
因为 res[i] 也是一个数组呀,push_back 是把 res[i] copy 一份然后添加到数组的最后,所以一次操作的时间是 O(N)。
综上,总的时间复杂度就是 O(N*2^N),还是比较耗时的。
空间复杂度的话,如果不计算储存返回结果所用的空间的,只需要 O(N) 的递归堆栈空间。如果计算 res 所需的空间,应该是 O(N*2^N)。
第二种通用方法就是回溯算法。旧文「回溯算法详解」写过回溯算法的模板:
1 | result = [] |
只要改造回溯算法的模板就行了:
1 | vector<vector<int>> res; |
可以看见,对 res 的更新是一个前序遍历,也就是说,res 就是树上的所有节点:
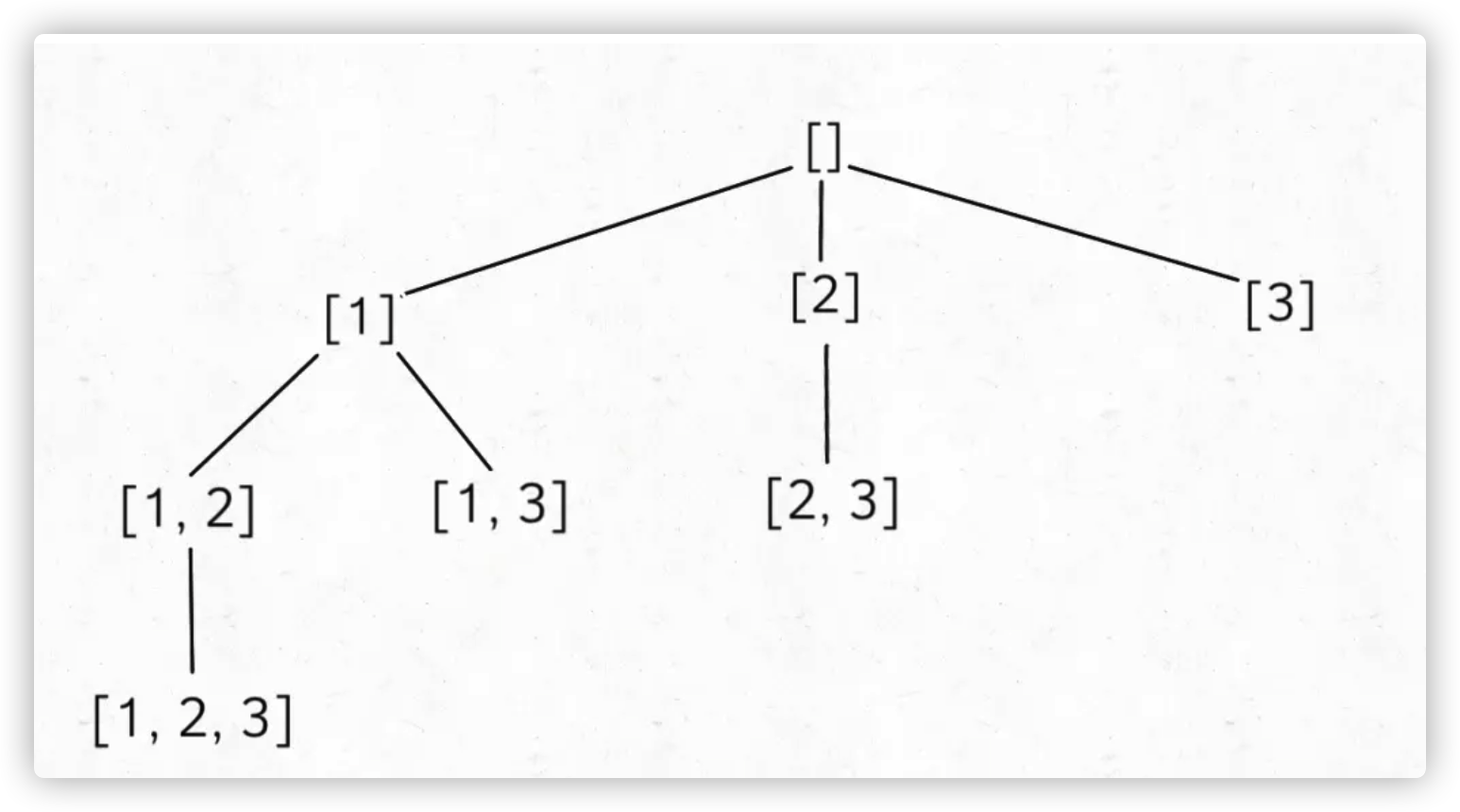
二、组合
输入两个数字 n, k,算法输出 [1..n] 中 k 个数字的所有组合。
1 | vector<vector<int>> combine(int n, int k); |
比如输入 n = 4, k = 2,输出如下结果,顺序无所谓,但是不能包含重复(按照组合的定义,[1,2] 和 [2,1] 也算重复):
[
[1,2],
[1,3],
[1,4],
[2,3],
[2,4],
[3,4]
]
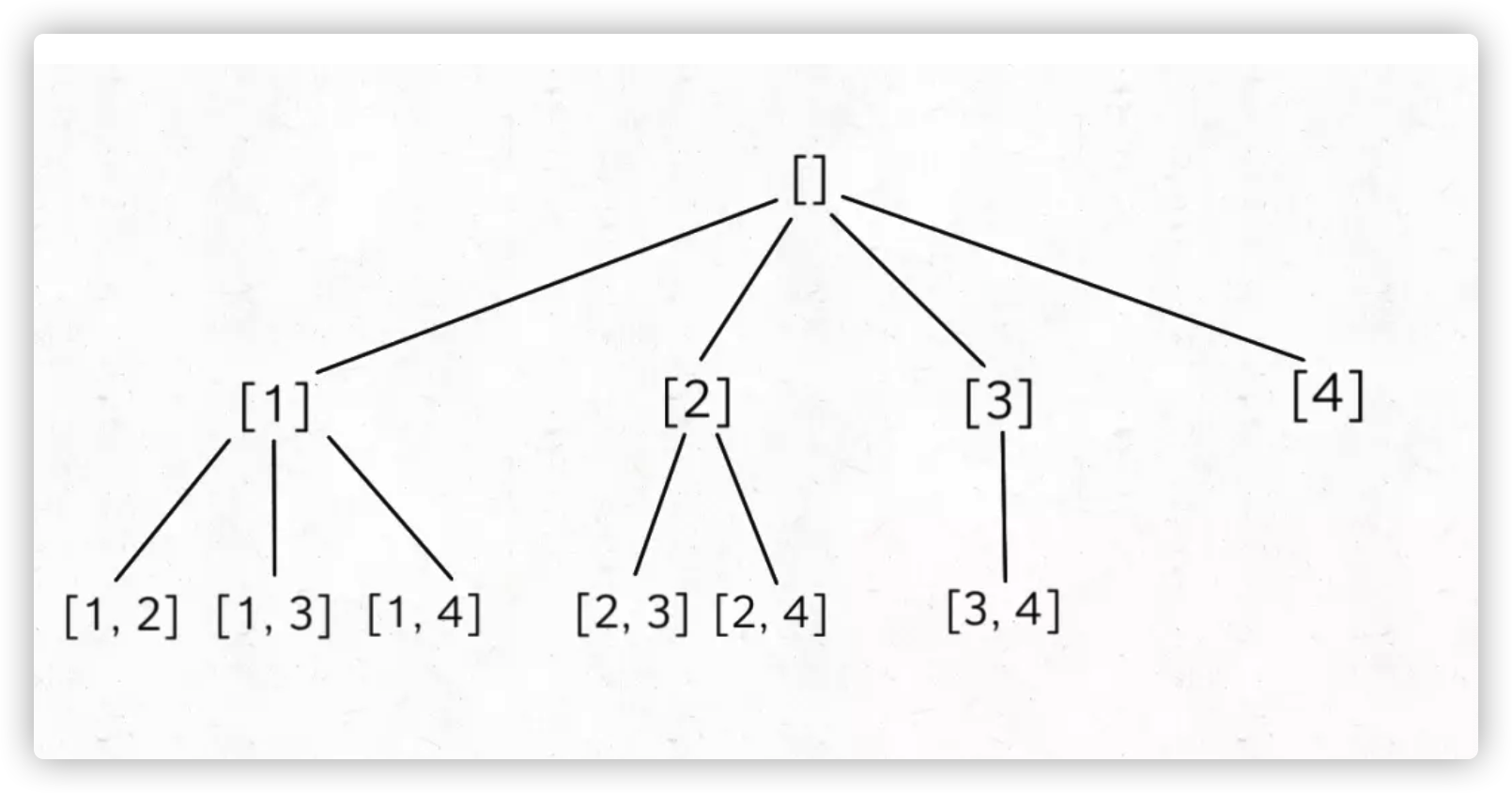
这就是典型的回溯算法,k 限制了树的高度,n 限制了树的宽度,直接套我们以前讲过的回溯算法模板框架就行了:
1 | vector<vector<int>>res; |
backtrack 函数和计算子集的差不多,区别在于,更新 res 的地方是树的底端。
三、排列
输入一个不包含重复数字的数组 nums,返回这些数字的全部排列。
1 | vector<vector<int>> permute(vector<int>& nums); |
比如说输入数组 [1,2,3],输出结果应该如下,顺序无所谓,不能有重复:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
回溯算法详解 中就是拿这个问题来解释回溯模板的。这里又列出这个问题,是将「排列」和「组合」这两个回溯算法的代码拿出来对比。
首先画出回溯树来看一看:
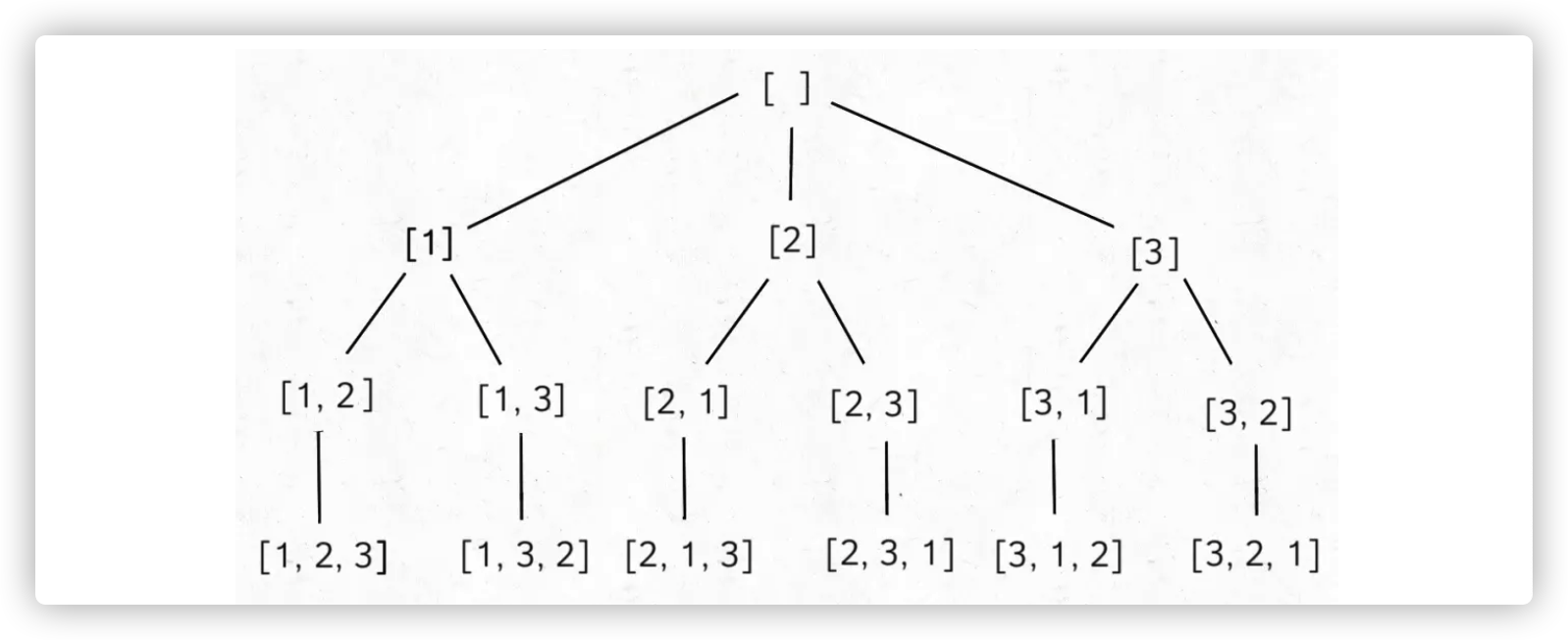
我们当时使用 Java 代码写的解法:
1 | List<List<Integer>> res = new LinkedList<>(); |
回溯模板依然没有变,但是根据排列问题和组合问题画出的树来看,排列问题的树比较对称,而组合问题的树越靠右节点越少。
在代码中的体现就是,排列问题每次通过 contains 方法来排除在 track 中已经选择过的数字;而组合问题通过传入一个 start 参数,来排除 start 索引之前的数字。
以上,就是排列组合和子集三个问题的解法,总结一下:
子集问题可以利用数学归纳思想,假设已知一个规模较小的问题的结果,思考如何推导出原问题的结果。也可以用回溯算法,要用 start 参数排除已选择的数字。
组合问题利用的是回溯思想,结果可以表示成树结构,我们只要套用回溯算法模板即可,关键点在于要用一个 start 排除已经选择过的数字。
排列问题是回溯思想,也可以表示成树结构套用算法模板,不同之处在于使用 contains 方法排除已经选择的数字,前文有详细分析,这里主要是和组合问题作对比。
对于这三个问题,关键区别在于回溯树的结构,不妨多观察递归树的结构,很自然就可以理解代码的含义了。