一个函数秒杀 2Sum 3Sum 4Sum 问题
一个函数秒杀 2Sum 3Sum 4Sum 问题
经常刷 LeetCode 的读者肯定知道鼎鼎有名的 twoSum 问题,我们的旧文 Two Sum 问题的核心思想 对 twoSum 的几个变种做了解析。
但是除了 twoSum 问题,LeetCode 上面还有 3Sum,4Sum 问题,我估计以后出个 5Sum,6Sum 也不是不可能。
那么,对于这种问题有没有什么好办法用套路解决呢?本文就由浅入深,层层推进,用一个函数来解决所有 nSum 类型的问题。
一、twoSum 问题
[leetcode1](1. 两数之和 - 力扣(LeetCode) (leetcode-cn.com))
力扣上的 twoSum 问题,题目要求返回的是索引,这里我来编一道 twoSum 题目,不要返回索引,返回元素的值:
如果假设输入一个数组 nums 和一个目标和 target,请你返回 nums 中能够凑出 target 的两个元素的值,比如输入 nums = [5,3,1,6], target = 9,那么算法返回两个元素 [3,6]。可以假设只有且仅有一对儿元素可以凑出 target。
我们可以先对 nums 排序,然后利用前文「双指针技巧汇总」写过的左右双指针技巧,从两端相向而行就行了:
1 | vector<int> twoSum(vector<int>& nums, int target) { |
这样就可以解决这个问题,不过我们要继续魔改题目,把这个题目变得更泛化,更困难一点:
nums 中可能有多对儿元素之和都等于 target,请你的算法返回所有和为 target 的元素对儿,其中不能出现重复。
函数签名如下:
1 | vector<vector<int>> twoSumTarget(vector<int>& nums, int target); |
比如说输入为 nums = [1,3,1,2,2,3], target = 4,那么算法返回的结果就是:[[1,3],[2,2]]。
对于修改后的问题,关键难点是现在可能有多个和为 target 的数对儿,还不能重复,比如上述例子中 [1,3] 和 [3,1] 就算重复,只能算一次。
首先,基本思路肯定还是排序加双指针:
1 | vector<vector<int>> twoSumTarget(vector<int>& nums, int target { |
但是,这样实现会造成重复的结果,比如说 nums = [1,1,1,2,2,3,3], target = 4,得到的结果中 [1,3] 肯定会重复。
出问题的地方在于 sum == target 条件的 if 分支,当给 res 加入一次结果后,lo 和 hi 不应该改变 1 的同时,还应该跳过所有重复的元素:
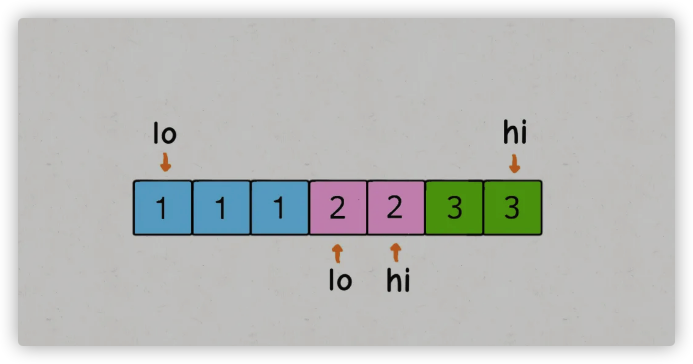
1 | while (lo < hi) { |
这样就可以保证一个答案只被添加一次,重复的结果都会被跳过,可以得到正确的答案。不过,受这个思路的启发,其实前两个 if 分支也是可以做一点效率优化,跳过相同的元素:
1 | vector<vector<int>> twoSumTarget(vector<int>& nums, int target) { |
这样,一个通用化的 twoSum 函数就写出来了,请确保你理解了该算法的逻辑,我们后面解决 3Sum 和 4Sum 的时候会复用这个函数。
这个函数的时间复杂度非常容易看出来,双指针操作的部分虽然有那么多 while 循环,但是时间复杂度还是 O(N),而排序的时间复杂度是 O(NlogN),所以这个函数的时间复杂度是 O(NlogN)。
二、3Sum 问题
这是力扣第 15 题「三数之和」:
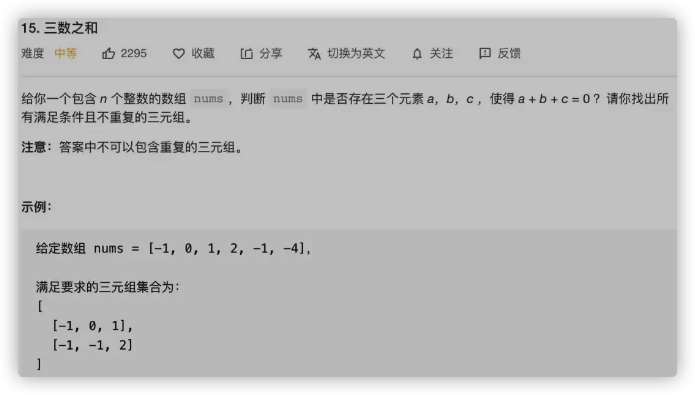
题目就是让我们找 nums 中和为 0 的三个元素,返回所有可能的三元组(triple),函数签名如下:
1 | vector<vector<int>> threeSum(vector<int>& nums); |
这样,我们再泛化一下题目,不要光和为 0 的三元组了,计算和为 target 的三元组吧,同上面的 twoSum 一样,也不允许重复的结果:
1 | vector<vector<int>> threeSum(vector<int>& nums) { |
这个问题怎么解决呢?很简单,穷举呗。现在我们想找和为 target 的三个数字,那么对于第一个数字,可能是什么?nums 中的每一个元素 nums[i] 都有可能!
那么,确定了第一个数字之后,剩下的两个数字可以是什么呢?其实就是和为 target - nums[i] 的两个数字呗,那不就是 twoSum 函数解决的问题么🤔
可以直接写代码了,需要把 twoSum 函数稍作修改即可复用:
1 | /* 从 nums[start] 开始,计算有序数组 |
需要注意的是,类似 twoSum,3Sum 的结果也可能重复,比如输入是 nums = [1,1,1,2,3], target = 6,结果就会重复。
关键点在于,不能让第一个数重复,至于后面的两个数,我们复用的 twoSum 函数会保证它们不重复。所以代码中必须用一个 while 循环来保证 3Sum 中第一个元素不重复。
至此,3Sum 问题就解决了,时间复杂度不难算,排序的复杂度为 O(NlogN),twoSumTarget 函数中的双指针操作为 O(N),threeSumTarget 函数在 for 循环中调用 twoSumTarget 所以总的时间复杂度就是 O(NlogN + N^2) = O(N^2)。
三、4Sum 问题
这是力扣第 18 题「四数之和」:

函数签名如下:
1 | vector<vector<int>> fourSum(vector<int>& nums, int target); |
都到这份上了,4Sum 完全就可以用相同的思路:穷举第一个数字,然后调用 3Sum 函数计算剩下三个数,最后组合出和为 target 的四元组。
1 | vector<vector<int>> fourSum(vector<int>& nums, int target) { |
这样,按照相同的套路,4Sum 问题就解决了,时间复杂度的分析和之前类似,for 循环中调用了 threeSumTarget 函数,所以总的时间复杂度就是 O(N^3)。
四、100Sum 问题?
在 LeetCode 上,4Sum 就到头了,但是回想刚才写 3Sum 和 4Sum 的过程,实际上是遵循相同的模式的。我相信你只要稍微修改一下 4Sum 的函数就可以复用并解决 5Sum 问题,然后解决 6Sum 问题……
那么,如果我让你求 100Sum 问题,怎么办呢?其实我们可以观察上面这些解法,统一出一个 nSum 函数:
1 | /* 注意:调用这个函数之前一定要先给 nums 排序 */ |
嗯,看起来很长,实际上就是把之前的题目解法合并起来了,n == 2 时是 twoSum 的双指针解法,n > 2 时就是穷举第一个数字,然后递归调用计算 (n-1)Sum,组装答案。
需要注意的是,调用这个 nSum 函数之前一定要先给 nums 数组排序,因为 nSum 是一个递归函数,如果在 nSum 函数里调用排序函数,那么每次递归都会进行没有必要的排序,效率会非常低。
比如说现在我们写 LeetCode 上的 4Sum 问题:
1 | vector<vector<int>> fourSum(vector<int>& nums, int target) { |
再比如 LeetCode 的 3Sum 问题,找 target == 0 的三元组:
1 | vector<vector<int>> threeSum(vector<int>& nums) { |
那么,如果让你计算 100Sum 问题,直接调用这个函数就完事儿了。